Intervals of Thirds – 2 Key Things to Understanding

You may have heard of the circle of fifths. It’s a very useful and helpful way to memorize 4th and 5th intervals. It’s a circle because it repeats over and over and, more simply, because one end carry over to the other: circular. The same, to a degree, is true for intervals of thirds.

Understanding Intervals of Thirds

If you’ve ever studied sheet music, you may have heard the phrase “Every Good Boy Does Fine” – that stands for the notes E-G-B-D-F. Those are the notes on staff of sheet music and their intervals of thirds.

The notes between the lines are F-A-C-E which obviously can be remembered with the word “face.”

How to Remember Thirds

As you can see, face ends with an E and that is the first note of the other set of intervals of thirds and you can repeat from there: F-A-C-E-G-B-D

And since E-G-B-D-F ends with F, you can repeat: F-A-C-E-G-B-D-F-A-C-E-G-B-D… a “circle” concept again for the intervals of thirds.

F-A-C-E-G-B-D – that’s not too much to memorize.

Since a major third interval is two whole steps, A’s major third is C#. So you do have to do some work to figure out exactly what you need. But F-A-C-E-G-B-D should help get you most of the way quickly.

Reverse for Sixths

If you go from right to left with these notes, you have sixths: A to F, for example. I decided to not even put the notes in reverse order here because I think it’s better to just memorize F-A-C-E-G-B-D

I just didn’t want to play a seed of seeing it in reverse. You can reverse it in your head as necessary.

Again, you have to account for the half-steps between B & C and E & F as necessary. And the same for doing minor intervals.

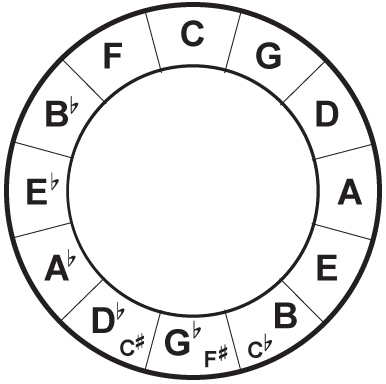
Circle of Fifths

The circle of fifths is a bit more to memorize, but it also gives you a lot more information.

9 is a Magic Number

Both circles for learning intervals have one interval for each direction. For intervals of thirds (F-A-C-E-G-B-D) has thirds going right and sixths going left. 3 + 6 = 9

The circle of fifths has fifths going right and fourths going left : 5 + 4 = 9

Of course if you did a circle for seconds (A-B-C-D-E-F-G) you would have seconds going right and sevenths going left: 2 + 7 = 9

These don’t take into consideration major/minor/flat/etc.

So the complimentary relationship of an interval is 9 – x where x is the interval. For the second interval A to B (2) the reverse (B to A) is 9 – x where x is 2 (the second) so it’s a seventh.

F to A is a third so 9 – 3 = 6 so A to F is a sixth.

Except for flat 5, one of the two needs to be a flat/minor. So the inverse of a 7 is a minor 2. Inverse of a minor 3 is 6. But inverse of flat 5 is flat 5.

The idea here is that if you know an interval for something, the reverse is 9 minus that interval. Just another handy tool for determining intervals.

1 Based Counting

You might be wondering: why is it 9? Why not 8 since that’s an octave. Good question!

This is due to 1-based counting.

When a baby is born, he is 0 years old. However, he is living his first (1) year. The first year is ‘year 1’ though he is not one year old yet.

After a year, the baby is 1 year old and living in his 2nd year. Years are 1-based and age is 0-based.

Confused?

Centuries are the same. 1-100 is the first century even though the second century (101-200) starts with 1. The 16th century is 1501-1600.

So for notes and intervals, C to D is a second interval – one whole step away. D to E is also a second – also one whole step away.

So if C-D is a second and D-E is a second, should C-E be a fourth? Nope, it’s a third.

Why?

Because when we started the second step, from C to E, we started at 1 again. The 1 is interval based but we’re concerned about steps. C to D is 1 whole step (second) and then D to E is 1 whole step (third).

Trying to add intervals adds an extra 1-based counting start for each interval that has to be accounted for.

This is getting a bit heavy and is covered in more depth in another post. But I like to plant good seeds when possible.

Conclusion

For now, memorize F-A-C-E-G-B-D as intervals of thirds going left to right (and sixths going right to left).